单调栈
首先,单调栈本身也属于栈,属于一个 “先进后出” 的数据结构。单调栈的话,就是需要栈内元素满足单调性的数据结构,可以是单调递增的,也可以是单调递减的。
对于数组 $[3,1,4,5,2,7]$ 为例,单调递增栈的过程如下:
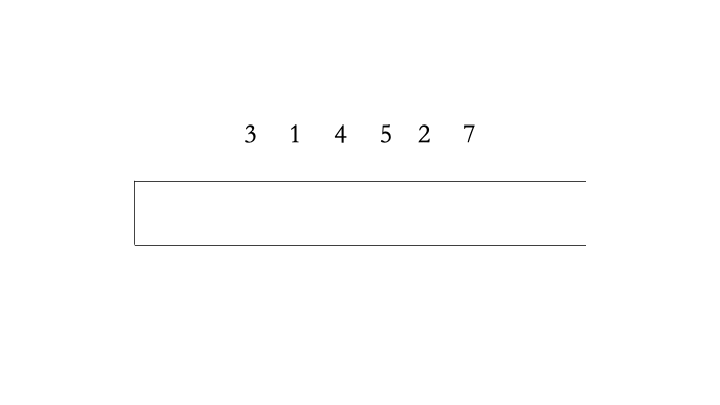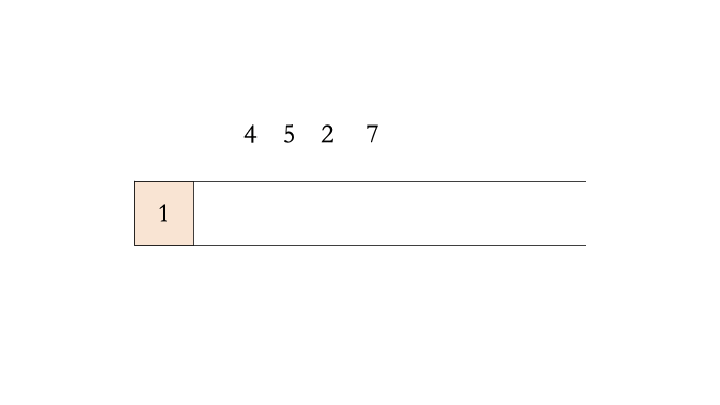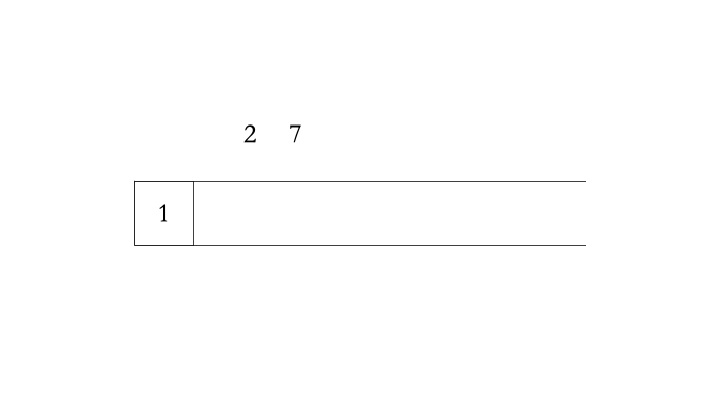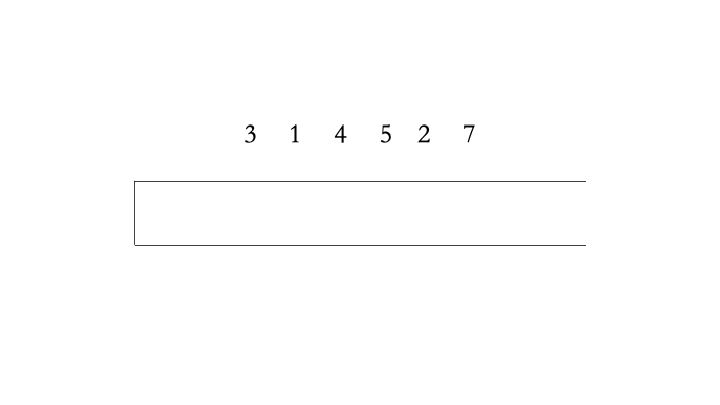
- acwing 131 直方图中最大矩形
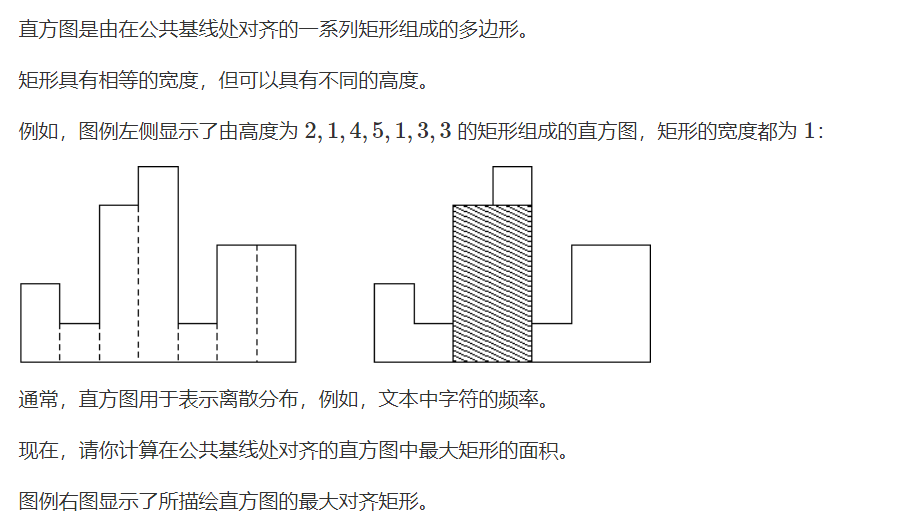
这道题的思路其实并不简单,我们要维护一个单调递增的栈。我们求解的过程是:遍历每个长方形的高,如果当前的遍历高度大于栈顶的高度,那就直接入栈。如果小于栈顶的高度,然后就不断的出栈,直到当前遍历高度大于栈顶的高度或者栈已经空了,在每次出栈的过程中,都会计算当前构成的矩形面积的值,并不断的更新最大值。
注意:这道题还需要存储每个高度对应的矩形的高度,所以用数组模拟栈比较方便操作,就不在使用STL中的stack数据结构。
#include <bits/stdc++.h>
using namespace std;
const int maxn = 1e5 + 1000;
typedef long long ll;
int n, cnt;
ll ans;
ll a[maxn], s[maxn], w[maxn];
int main() {
while (scanf("%d", &n) && n != 0) {
a[n + 1] = 0;
cnt = 0;
ans = 0;
// 用数组s模拟栈的情况
memset(s, 0, sizeof(s));
memset(w, 0, sizeof(w));
for (int i = 1; i <= n; ++i) cin >> a[i];
// 这里n + 1的原因是为了让最后一个入栈的元素能够计算
for (int i = 1; i <= n + 1; ++i) {
if (a[i] > s[cnt]) {
s[++cnt] = a[i];
w[cnt] = 1;
} else {
int width = 0;
while (s[cnt] > a[i]) {
// 不断更新该状态下对应的矩形面积
width += w[cnt];
ans = max(ans, (ll) width * s[cnt]);
cnt--;
}
s[++cnt] = a[i];
w[cnt] = width + 1;
}
}
printf("%lld\n", ans);
}
return 0;
}- LeetCode 503 下一个更大元素
题目要求:给定一个循环数组(最后一个元素的下一个元素是数组的第一个元素),输出每个元素的下一个更大元素。数字 x 的下一个更大的元素是按数组遍历顺序,这个数字之后的第一个比它更大的数,这意味着你应该循环地搜索它的下一个更大的数。如果不存在,则输出 -1。
把两个nums数组拼接在一起,使用单调栈计算出每一个元素的下一个最大值,最后再把结果集即result数组resize到原数组大小就可以了。
// 版本一
class Solution {
public:
vector<int> nextGreaterElements(vector<int>& nums) {
// 拼接一个新的nums
vector<int> nums1(nums.begin(), nums.end());
nums.insert(nums.end(), nums1.begin(), nums1.end());
// 用新的nums大小来初始化result
vector<int> result(nums.size(), -1);
if (nums.size() == 0) return result;
// 开始单调栈
stack<int> st;
for (int i = 0; i < nums.size(); i++) {
while (!st.empty() && nums[i] > nums[st.top()]) {
result[st.top()] = nums[i];
st.pop();
}
st.push(i);
}
// 最后再把结果集即result数组resize到原数组大小
result.resize(nums.size() / 2);
return result;
}
};单调队列
单调队列与单调栈相似,他们的区别在于单调栈只能从一端进行元素的添加和删除,而单调队列可以维护数组两端元素的添加和删除。
c++ STL中有一个数据结构 $deque$,可以实现双端队列的效果。即可以在队列的两端进行元素的添加和删除,用来维护单调队列比较方便。(当然也可以直接通过数组进行维护)。
关于单调队列,最经典的就是滑动窗口模型。
- acwing 154 滑动窗口
题目:给定一个大小为 $n <= 10^6$ 的数组。有一个大小为 $k$ 的滑动窗口,它从数组的最左边移动到最右边。你只能在窗口中看到 $k$ 个数字。你的任务是确定滑动窗口位于每个位置时,窗口中的最大值和最小值。
#include <bits/stdc++.h>
using namespace std;
const int N = 1005;
int a[N];
deque<int> q;
int main()
{
int n, m;
cin >> n >> m;
for(int i = 1; i <= n; i++) {
cin >> a[i];
}
// 单调队列维护窗口最小值
for(int i = 1; i <= n; i++) {
// 如果当前队列尾部的值大于当前遍历的值,就不断的弹出尾部的值
while(!q.empty() && a[q.back()] >= a[i]) {
q.pop_back();
}
// 如果当前队列头部的索引已经超过了滑动窗口的限制,弹出头部的值
while(q.front() <= i - m) {
q.pop_front();
}
q.push_back(i);
// 输出每个窗口对应的最小值
if(i >= m) cout << a[q.front()] << " ";
}
cout << "\n";
q.clear();
for(int i = 1; i <= n; i++) {
while(!q.empty() && a[q.back()] <= a[i]) {
q.pop_back();
}
while(q.front() <= i - m) {
q.pop_front();
}
q.push_back(i);
if(i >= m) cout << a[q.front()] << " ";
}
return 0;
}- acwing 135 最大子序和
题目:输入一个长度为 $n$ 的整数序列,从中找出一段长度不超过 $m$ 的连续子序列,使得子序列中所有数的和最大。

#include <bits/stdc++.h>
using namespace std;
const int N = 1005;
int a[N], sum[N];
deque<int> q;
int res;
// 单调队列优化算法,算法复杂度为o(n)
int main()
{
int n, m;
cin >> n >> m;
for(int i = 1; i <= n; i++) {
cin >> a[i];
sum[i] = sum[i - 1] + a[i];
}
q.push_back(0);
for(int i = 1; i <= n; i++) {
// 如果子序列的长度超过了m, 弹出队列头部的值
while(!q.empty() && q.front() < i - m) {
q.pop_front();
}
res = max(res, sum[i] - sum[q.front()]);
// 如果当前遍历的值的前缀和小于队列尾部的前缀和,弹出尾部的值
// 原因是区间和是s[R] - s[L],所以s[L]肯定要越小越好。
while(!q.empty() && sum[q.back()] >= sum[i]) {
q.pop_back();
}
q.push_back(i);
}
cout << res << endl;
return 0;
}


